Содержание

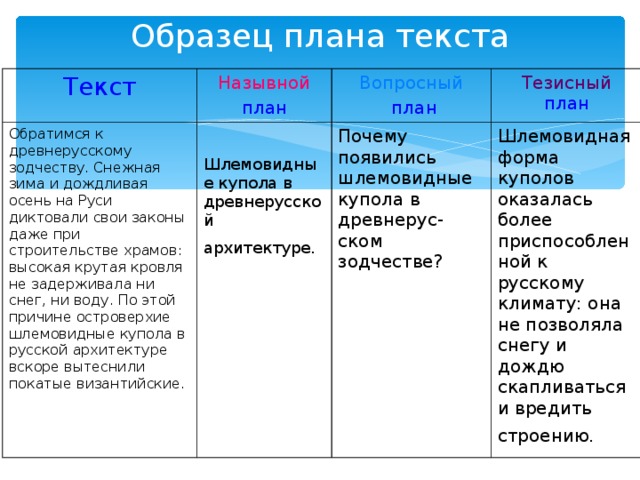
Составление плана текста с обозначенными частями.

Коррекционное развитие речи

25.11 Тема урока: Составление плана текста с обозначенными частями.

Здравствуйте, ребята! Сегодня на уроке я продолжу знакомить вас с таким понятием, как «план текста», а также научу составлять простые и сложные планы:

Для начала поговорим о том, что такое план:

План — это последовательное представление частей содержания изученного текста в кратких формулировках, отражающих тему и/или основную мысль.

  • Тема — это исходный пункт текста или его части, то, относительно чего нечто утверждается или спрашивается.

  • Основная мысль — это то, что утверждается или спрашивается о теме.

Для чего нужно уметь составлять план текста?

«…Работать над планом – это значит проникать в смысл читаемого, изучать построение произведения, вникать в его язык и в его образы» М. А. Рыбникова


В основном планы делятся на два типа:

Планы бывают

Простой план — это план, включающий название значительных частей текста. Графическая форма записи простого плана выглядит следующим образом:

1.

2.

3. и т.д.

Сложный план — это план, включающий название значительных частей текста, а также их смысловых компонентов. Графическая форма записи сложного плана выглядит следующим образом:

1.

1.1.

1.2.

2. и т.д.

Как составить план текста

Прочитай текст целиком.

2. Раздели текст на смысловые части. Начало и конец отметь карандашом (одна часть от другой отмечается новым содержанием).

3. Прочитай первую часть, выдели главное. Подбери к ней заголовок.

4. Таким образом, поработай над другими частями.

5. Запиши заголовки к каждой части (план).

6. Проверь себя:

— отражает ли заголовок главное в части текста:

-не повторяются ли заголовки;

-не пропущено ли что-либо важное;

— помогут ли твои заголовки.

А теперь давайте на примерах попробуем составить план:

Прочитайте текст всем известной детской сказки:

Колобок

Жили-были старик со старухой. Однажды просит старик:

— Испеки, старуха, колобок.

— Из чего испечь-то? Муки нет.

— Эх, старуха! По коробу поскреби, по сусеку помети; авось муки и наберется.

Старуха по коробу поскребла, по сусеку помела, и набралось муки две пригоршни. Замесила на сметане, пожарила в масле и положила на окошечко остудить.

Колобок полежал-полежал, да вдруг и покатился — с окна на лавку, с лавки на пол, по полу да к дверям, перепрыгнул через порог в сени, из сеней на крыльцо, с крыльца на двор, со двора за ворота, дальше и дальше.

Катится колобок по дороге, а навстречу ему заяц:

— Колобок, колобок! Я тебя съем!

— Не ешь меня, косой зайчик! Я тебе песенку спою, — сказал колобок и запел:

Я по коробу скребен,
По сусеку метен,
На сметане мешон
Да в масле пряжон,
На окошке стужон;
Я от дедушки ушел,
Я от бабушки ушел,
От тебя, зайца, не хитро уйти!

И покатился себе дальше; только заяц его и видел!. .

Катится колобок, а навстречу ему волк:

— Колобок, колобок! Я тебя съем!

— Не ешь меня, серый волк! Я тебе песенку спою!

Я по коробу скребен,
По сусеку метен,
На сметане мешон
Да в масле пряжон,
На окошке стужон;
Я от дедушки ушел,
Я от бабушки ушел,
Я от зайца ушел,
От тебя, волка, не хитро уйти!

И покатился себе дальше; только волк его и видел!..

Катится колобок, а навстречу ему медведь:

— Колобок, колобок! Я тебя съем.

— Где тебе, косолапому, съесть меня!

Я по коробу скребен,
По сусеку метен,
На сметане мешон
Да в масле пряжон,
На окошке стужон;
Я от дедушки ушел,
Я от бабушки ушел,
Я от зайца ушел,
Я от волка ушел,
От тебя, медведь, не хитро уйти!

И опять укатился; только медведь его и видел!..

Катится, катится колобок, а навстречу ему лиса:

— Здравствуй, колобок! Какой ты хорошенький!

А колобок запел:

Я по коробу скребен,
По сусеку метен,
На сметане мешон
Да в масле пряжон,
На окошке стужон;
Я от дедушки ушел,
Я от бабушки ушел,
Я от зайца ушел,
Я от волка ушел,
От медведя ушел,
От тебя, лиса, и подавно уйду!

— Какая славная песенка! — сказала лиса. — Но ведь я, колобок, стара стала, плохо слышу; сядь-ка на мою мордочку да пропой еще разок погромче.

Колобок вскочил лисе на мордочку и запел ту же песню.

— Спасибо, колобок! Славная песенка, еще бы послушала! Сядь-ка на мой язычок да пропой в последний разок, — сказала лиса и высунула свой язык.

Колобок прыг ей на язык, а лиса — ам его! — и скушала.

  • Составляем простой план, то есть план, включающий название частей текста, в которых содержится главный смысл. Чтобы не выписывать просто предложения из текста, мы придумываем заголовки к каждой части, которую выделили.

Например, к данной сказке можно составить такой простой план:

  1. Появление Колобка

  2. Бегство Колобка

  3. Встреча с зайцем

  4. Встреча с медведем

  5. Встреча с лисой

  6. Гибель Колобка

  • А теперь попробуем составить сложный план, то есть план в котором содержание темы поделено на разделы (пункты), подразделы (подпункты)

Например, к данной сказке можно составить такой сложный план:

  1. Появление Колобка:

1. Жизнь деда с бабкой до появления Колобка

2. «По сусекам помела» — рецепт появления новой формы жизни

  1. Бегство Колобка

  2. Встречи Колобка

1. С зайцем

2. С медведем

3. С Лисой

а) приветствие…

б) хитрость лисы

IV. Гибель Колобка

Таким образом, сегодня мы с вами познакомились с такими типами планов текста как простые и сложные, попробовали на примере сказки составить и простой и сложный план.

Домашнее задание: составьте простой план к данному рассказу:

План текста — виды (простой, сложный тезисный) — «Семья и Школа»

Содержание

Как сделать простой план?

Как сделать простой план?

Как составлять простой план.

  1. Прочтите текст (представьте мысленно весь материал).
  2. Разделите текст на части и выделите в каждой из них главную мысль.
  3. Озаглавьте части; подбирая заголовки, замените глаголы именами существительными.
  4. Прочитайте текст во второй раз и проверьте, все ли главные мысли отражены в плане.

Как составить сложный план к тексту?

Как составить сложный план.

  1. Внимательно прочитайте изучаемый материал.
  2. Разделите его на основные смысловые части и озаглавьте их (пункты плана).
  3. Разделите на смысловые части содержание каждого пункта и озаглавьте (подпункты плана).

Что такой сложный план?

Сложный план Представляет собой более совершенную систему, которая достаточно полно отражает работу автора над текстом и дает читателю ясное преставление о логике и композиции работы. В сложном плане практически каждый пункт имеет подпункты, в которых тема раскрывается более детально.

Что передает план текста?

Что передаёт план текста? План очень коротко передает основное содержание текста. План очень коротко определяет заглавие текста. План очень коротко определяет основную мысль текста.

Что такое тезис план?

Тезисный план — план из тезисов глагольного строя (например: Многие животные и птицы пользуются звуками, которые мы не слышим). Тезис — это кратко сформулированное основное положение абзаца, текста лекции, доклада и т. п. Тезисы обычно совпадают с информативным центром абзаца.

Что такое пункт плана?

Пункты плана – это ориентиры, которые помогают автору двигаться в нужном направлении – к задаче, поставленной перед текстом. Текст, написанный без плана, напоминает поток сознания. Невозможно уловить его центральную идею, а следить за развитием мысли – крайне сложно.

Что такое сложный план к тексту?

План текста – это последовательный и связный перечень основных мыслей, которые автор в нем высказывает. Он необходим школьнику для того, чтобы понять, о чем говорил автор, а также лучше запомнить все то, что изложено в его произведении.

Что такое план по тексту?

План текста — это перечень основных мыслей, расположенных в такой последовательности, которая отражает логику текста. Чтобы составить план, весь текст нужно разделить на микротемы (как правило, это абзацы текста), каждая из которых объединена определённой мыслью и имеет логическую завершённость.

Что такое план текста 5 класс?

Это краткая и лаконичная мысль небольшого отрывка текста, сформулированная в одном или двух предложениях. … Правильно составленный тезисный план представляет собой лаконичный и последовательный сжатый текст исходного материала.

Как правильно составить план?

Метод первый. Создайте план на день

  1. Сядьте с листом бумаги …
  2. Составьте себе расписание …
  3. Переориентируйте себя каждый час …
  4. Проанализируйте ваш день …
  5. Создайте общие цели, которые вы хотите достичь в вашей жизни …
  6. Создайте некоторые конкретные цели с определённой датой выполнения

Как правильно планировать на год?

6 советов, как правильно планировать на год

  1. Планируйте в удобное время Неважно, когда вы это сделаете и сколько времени займет планирование. …
  2. Составьте колесо баланса …
  3. Цели должны вдохновлять …
  4. Планируйте четко и тактично …
  5. Следуйте своему пути …
  6. Не бойтесь корректировать свой план

В каком времени ставить цели?

Цель должна быть написана в настоящем времени как уже сбывшийся факт. Чаще всего цели пишут в будущем времени: «умею водить машину», «знаю английский» и т. д. Правильно написанная цель будет сформулирована как «веду машину», «разговариваю на английском языке с американцем».

Почему нужно писать цели на бумаге?

Одной из основных причин того, что запись целей способствует их исполнению, является факт визуального изображения на бумаге. То есть, все о чем вы мечтаете, остается мечтами до тех пор, пока вы не пропишите это и не трансформируете в конкретные задачи.

В каком случае ставится am is are?

Таким образом, am можно использовать только с I, ни в каком другом случае. Are ставим, если в роли подлежащего you, we, they и слова, которые можно заменить этими местоимениями (people, eggs, “you and I” и т. д.) Is появляется только после he, she, it и слов, заменяемых ими (Kate, a boy, an apple, a cow и т.

Когда нужно писать IS?

Опорным в понимании логики грамматического закона должны быть не слова-местоимения, а понятия. Например, можно сформулировать так: «“Am” – когда я показываю на себя одного, “is” – когда показываю на кого-то одного, “are” – для многих».

Как составить план текста — рекомендации по составлению плана с примерами

Прежде чем приступать к написанию статьи, автору необходимо понять, что именно и в каком порядке он собирается описывать. В этом помогает план текста – изложенные в виде списка и логически структурированные основные мысли статьи.

Давайте разберемся, как составить план текста, поговорим о видах планов и требованиях, которые необходимо соблюдать при их написании.

Зачем нужен план текста?

  • План облегчает автору задачу и значительно ускоряет процесс написания текста, избавляет от страха белого листа.
  • Закончив одну часть статьи, вам не придется думать, о чем рассказывать дальше – достаточно посмотреть в план и раскрыть следующий пункт.
  • План не даст запутаться, отступить от темы, поможет более четко и доступно для читателя сформулировать свои мысли.
  • Кроме того, если вы пишете тексты на заказ, после составления плана вы можете согласовать его с заказчиком, дабы тот убедился, что вы правильно поняли свою задачу.

Комьюнити теперь в Телеграм

Подпишитесь и будьте в курсе последних IT-новостей

Подписаться

Особенности написания плана

Прежде чем приступить к написанию плана текста, внимательно изучите всю найденную информацию по теме, а затем выделите основную идею. Задумайтесь о том, какую задачу должна решать статья, на какой вопрос читателя отвечать. Информация, которая содержит ответ на вопрос, и определит структуру текста.

Собранные для написания текста сведения необходимо разделить на несколько частей, разбить на смысловые блоки, выделить логические категории для удобства восприятия информации.

Поставьте себя на место читателя, обратившегося к вашей статье для решения своей проблемы. Подумайте, какие именно данные будут наиболее важны для него и какие советы могут быть максимально полезны. Теперь опишите все это в виде последовательности пунктов, и ваш план будет готов, а дальше можно приступать к написанию и редактированию материала.

При составлении плана нужно учитывать характер текста. Например, при написании новостей и обзоров в первых пунктах плана нужно отразить самые важные, привлекающие внимание данные, в середине статьи подробно раскрыть изложенные в начале сведения, а в конце расположить обобщение или дополнительную информацию. Тогда как при написании научных статей автор, наоборот, сначала излагает аргументы, ссылается на авторитетные источники и только в конце текста озвучивает основную идею материала.

Виды планов текста

Статья состоит из заголовка, введения, основной части и заключения. Рассмотрим, какие виды планов позволяют структурировать информацию основной части текста.

Назывной план

Назывной план состоит из небольших заголовков, включающих обычно от 2 до 4 слов. Глаголы в таком типе плана не используются, содержание пунктов выражается существительными в именительном падеже и прилагательными. Каждый пункт такого плана состоит из опорных слов и словосочетаний, которые отражают какой-то процесс, явление либо состояние.

Пример назывного плана для данной статьи:

  1. Назначение плана текста.
  2. Особенности написания плана.
  3. Виды планов текста.
  4. Требования к плану текста.
Вопросный план

Структура плана этого типа основана на вопросах, которые автор задает к каждому смысловому блоку текста. На мой взгляд, это самый простой вариант плана, так как уже в процессе обдумывания темы и сбора материала для статьи вопросы возникают сами собой. Этот вариант идеально подойдет, если вы пишете руководство, инструкцию или обучающую статью. Начинайте вопросительные предложения со слов: как, когда, почему, какой, сколько, кто, каким образом и т.

 п.

Например, к текущей статье вопросный план может быть таким:

  1. Зачем нужен план текста?
  2. В чем заключаются особенности написания плана?
  3. Какие существуют виды планов текста?
  4. Как проверить правильность составления плана?
Тезисный план

Тезисный план – это план, состоящий из тезисов, как и назывной, однако здесь обязательно используются глаголы, из-за чего пункты получаются длиннее. Тезис представляет собой основную мысль нескольких абзацев, которая сформулирована в одном предложении. Подлежащее в каждом пункте обозначает тему, а сказуемое раскрывает ее.

На каждую тысячу знаков рекомендует отводить один пункт в тезисном плане. Соответственно, если в статье 5000 знаков, пунктов-тезисов должно быть 5.

Рассмотрим, что такое тезисный план на примере этой статьи:

  1. Причины, по которым имеет смысл составлять план текста.
  2. Действия, которые необходимо выполнить в начале написания плана.
  3. Нюансы, которые необходимо учесть при составлении плана в зависимости от характера текста.
  4. Виды планов могут быть разными и каждый подходит для определенных типов текста.
  5. Требования, которым должен соответствовать правильно составленный план.
Опорный план

Опорный план-схема характерен тем, что в качестве его пунктов используются только ключевые мысли, самые значимые слова или отрывки предложений, на которые автор будет опираться при написании текста. План этого типа хорошо подходит для составления текста устного выступления, презентации, а также при написании различных небольших по объему текстов, таких как новости, анонсы, краткие обзоры и т.п.

В опорную схему уместно включить главные факты, цифры, названия предметов, а также имена действующих лиц и цитаты. Каждый пункт данного плана является опорой, вызывающей яркие, детальные картины, которые передают содержание текста. Назначение этого вида плана – систематизация собранного материала и облегчение последующего воспроизведения информации. Пункты в таком плане могут существенно отличаться друг от друга как по структуре, так и по длине.

Пример опорного плана:

  1. 4 причины целесообразности написания плана текста.
  2. Какие особенности надо учитывать при написании плана.
  3. 5 видов планов текста с примерами.
  4. В каких случаях можно обойтись простым, а когда нужен сложный план.
  5. Чек-лист проверки правильности составления плана текста.
Смешанный план

Совсем необязательно стремиться к тому, чтобы все пункты плана представляли собой вопросы или являлись тезисами статьи, можно составить план смешанного типа. Например:

  1. Зачем нужен план текста?
  2. Особенности написания плана.
  3. Какие существуют виды планов текста?
  4. Чек-лист проверки правильности составления плана.
Простые и сложные планы текста

Планы текста по своему типу также можно разделить на простые и сложные.

Сложный план отличается большей развернутостью и содержит подпункты. Это необходимо, если статья содержит мысли разного уровня, когда определенная мысль раскрывается посредством нескольких других. Используйте сложные планы с пронумерованными пунктами и подпунктами, оформленными как маркированный список, для длинных серьезных статей со множеством подзаголовков – в этом случае вы не упустите из вида ни одну даже самую мелкую деталь.

В других случаях можно ограничиться составлением простого плана, в котором пункты располагаются последовательно.

Сложный план для данной статьи может выглядеть так:

  1. Зачем нужен план текста?
  2. В чем заключаются особенности написания плана?
    • С чего начинается составление плана
    • Зависимость от характера текста
  3. Какие существуют виды планов текста?
    • Назывной план
    • Вопросный план
    • Тезисный план
    • Опорная схема
    • Смешанный тип
    • Простые и сложные планы текста
  4. Как проверить правильность составления плана?

Требования к плану текста

Правильно составленный план текста должен соответствовать ряду требований:

Заключение

Итак, мы рассмотрели, что такое план текста, и убедились, что его использование делает работу над статьей намного продуктивнее. При наличии грамотно составленного плана вы напишете текст быстрее и качественнее. План позволяет легко сфокусироваться на теме, в процессе его составления в голове автора вырисовывается четкая картина того, как должен выглядеть готовый текст и на какие вопросы читателя он будет отвечать.

Выбирайте тот тип плана, что наилучшим образом соответствует виду текста, который вам предстоит написать. И помните, что при составлении плана информационной статьи вы не обязаны неукоснительно придерживаться какого-то одного из типов и видов.

ПРОСТЫЕ пенсионные планы для мелких работодателей Определение

Оглавление

Содержание

  • Что такое ПРОСТОЙ план?

  • Понимание простых планов

  • Два варианта выбора работодателя

  • Ограничения плана SIMPLE

  • Часто задаваемые вопросы

По

Юлия Каган

Полная биография

Юлия Каган пишет о личных финансах более 25 лет, а для Investopedia с 2014 года. Бывший редактор Consumer Reports , она является экспертом по кредитам и долгам, планированию выхода на пенсию, домовладению, вопросам занятости и страхованию. Она окончила Брин-Мор-колледж (бакалавр истории) и имеет степень магистра искусств в области документальной литературы в Беннингтон-колледже.

Узнайте о нашем редакционная политика

Обновлено 02 февраля 2022 г.

Рассмотрено

Дэвид Доброта

Рассмотрено Дэвид Кинднесс

Полная биография

Дэвид Кинднесс является сертифицированным бухгалтером (CPA) и экспертом в области финансового учета, корпоративного и индивидуального налогового планирования и подготовки, а также инвестирования и пенсионного планирования. Дэвид помог тысячам клиентов улучшить свои бухгалтерские и финансовые системы, составить бюджет и минимизировать налоги.

Узнайте о нашем Совет финансового контроля

Факт проверен

Викки Веласкес

Факт проверен Викки Веласкес

Полная биография

Викки Веласкес — исследователь и писатель, которая руководила, координировала и руководила различными общественными и некоммерческими организациями. Она провела углубленное исследование социальных и экономических вопросов, а также пересмотрела и отредактировала учебные материалы для района Большого Ричмонда.

Узнайте о нашем редакционная политика

Что такое план поощрения сбережений для сотрудников мелких работодателей (ПРОСТОЙ)?

План сбережений для сотрудников мелких работодателей (SIMPLE) — это тип пенсионного счета с отсрочкой уплаты налогов, который может открываться работодателями, в том числе самозанятыми. Работодателю разрешен налоговый вычет для взносов, сделанных на счет SIMPLE.

Работодатель может вносить долевые или необязательные взносы в SIMPLE IRA каждого правомочного сотрудника, а сотрудники могут вносить отсроченные взносы по зарплате.

Key Takeaways
  • План поощрения сбережений для сотрудников мелких работодателей (SIMPLE) — это пенсионный счет с отсрочкой уплаты налогов, который позволяет мелким работодателям вносить вклад в пенсионные сбережения своих сотрудников и свои собственные пенсионные сбережения.
  • Только работодатели, которые не предлагают другие пенсионные планы и имеют менее 100 сотрудников, могут создавать и предлагать SIMPLE IRA.
  • SIMPLE IRAs легче создать работодателю, и они имеют более низкие административные и начальные расходы, чем многие другие пенсионные планы.
  • ПРОСТЫЕ IRA требуют от работодателей внесения минимального взноса на счет работника.
  • Годовой взнос работодателя может быть либо долевым взносом в размере до 3% от компенсации, либо неизбирательным взносом в размере 2% за каждого правомочного работника.

Понимание простых планов

План сбережений для сотрудников мелких работодателей (SIMPLE) — это спонсируемый работодателем пенсионный план, в некотором роде похожий на планы 401(k) и 403(b). ПРОСТЫЕ IRA легче реализовать и имеют более низкие начальные и административные расходы, чем многие другие пенсионные планы. У работодателя нет требований к подаче заявления в SIMPLE IRA.

Согласно правилам Налоговой службы (IRS), только работодатели с менее чем 100 сотрудниками, которые не предлагают другие пенсионные планы, могут создать ПРОСТОЙ IRA. Все сотрудники, получившие компенсацию в размере 5000 долларов США или более от работодателя в течение любых двух предыдущих календарных лет и которые, как ожидается, получат компенсацию в размере 5000 долларов США или более в этом году, имеют право участвовать в плане SIMPLE IRA работодателя.

SIMPLE IRA имеет те же правила в отношении инвестиций, распределений и пролонгаций, что и традиционные индивидуальные пенсионные счета (IRA).

Две альтернативы работодателя

ПРОСТЫЕ IRA требуют, чтобы работодатели вносили минимальный взнос на счет, в то время как сотрудники не обязаны вносить взносы. У работодателя есть две альтернативы, когда дело доходит до внесения этих взносов. Первый заключается в том, чтобы сопоставить суммы, которые сотрудники вносят в счет своих собственных отсрочек, до 3 % от годового вознаграждения сотрудника.

Второй вариант заключается в том, чтобы работодатель вносил фиксированный неизбирательный взнос в размере 2% за всех квалифицированных сотрудников, независимо от того, делает ли сотрудник какие-либо взносы.

Взносы в SIMPLE IRAs сразу же на 100% переходят в собственность, и владелец IRA направляет инвестиции.

Ограничения плана SIMPLE

План поощрения сбережений для сотрудников мелких работодателей (SIMPLE) имеет более низкие лимиты взносов, чем большинство других пенсионных планов, спонсируемых работодателем. На 2022 год лимит взносов составляет 14 000 долларов США (по сравнению с 13 500 долларов США в 2021 году). Лица в возрасте 50 лет и старше могут внести дополнительный взнос в размере 3000 долларов США как в 2021, так и в 2022 году.

Простой IRA может быть преобразован в традиционный IRA только после двухлетнего периода ожидания, начиная со дня, когда сотрудник впервые принял участие в плане.

Как работодателю начать план SIMPLE IRA?

Чтобы начать план SIMPLE IRA, необходимо выполнить три шага:

  1. Подписать форму IRS 5304-SIMPLE, форму 5305-SIMPLE или утвержденный IRS прототип плана SIMPLE IRA, предлагаемый квалифицированным финансовым учреждением.
  2. Предоставить правомочным сотрудникам информацию о плане SIMPLE IRA.
  3. Создайте простую учетную запись IRA для каждого подходящего сотрудника, используя учетную запись хранителя или трастовую учетную запись.

Какие сотрудники могут участвовать в плане SIMPLE?

Чтобы иметь право участвовать в плане SIMPLE от работодателя на календарный год, работник должен получить компенсацию в размере не менее 5000 долларов от работодателя в течение любых двух предшествующих календарных лет (независимо от того, идут они подряд или нет). Работник также должен обоснованно ожидать, что он заработает не менее 5000 долларов США в качестве компенсации за календарный год.

При определенных обстоятельствах работодатель может исключить работника из плана SIMPLE. Например, работодатель может принять решение об исключении работников, на которых распространяются определенные типы коллективных договоров.

Могут ли сотрудники отказаться от плана SIMPLE IRA?

Нет, правомочные сотрудники не могут отказаться от участия в плане SIMPLE IRA работодателя. Однако они могут принять решение не делать взносы в план, которые уменьшат их заработную плату. В этом случае они не получат никаких соответствующих взносов, если их предложит работодатель. Они будут получать невыборные взносы от работодателя, если план предлагает это.

Источники статей

Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами. Мы также при необходимости ссылаемся на оригинальные исследования других авторитетных издателей. Вы можете узнать больше о стандартах, которым мы следуем при создании точного и беспристрастного контента, в нашем редакционная политика.

  1. Налоговая служба. «Публикация 560, Пенсионные планы для малого бизнеса (SEP, SIMPLE и квалифицированные планы)», стр. 9-11.

  2. Налоговая служба. «ПРОСТОЙ ИРА план».

  3. Налоговая служба. «IRS объявляет об увеличении лимита 401 (k) до 20 500 долларов».

  4. Налоговая служба. «Часто задаваемые вопросы по плану SIMPLE IRA», выберите «Пролонгация».

  5. Налоговая служба. «Часто задаваемые вопросы по плану SIMPLE IRA», выберите «Создание плана SIMPLE IRA».

  6. Налоговая служба. «Часто задаваемые вопросы по плану SIMPLE IRA», выберите «Участие».

  7. Налоговая служба. «Часто задаваемые вопросы о плане SIMPLE IRA», выберите «Может ли участник «отказаться» от плана SIMPLE IRA?»

Что такое ПРОСТОЙ план

План Savings Incentive Match для сотрудников (ПРОСТОЙ план) представляет собой письменное соглашение, которое предоставляет вам, как работодателю, и вашим сотрудникам упрощенный способ внесения взносов для обеспечения пенсионного дохода.

ПРОСТОЙ план позволяет мелкому работодателю избежать сложностей правил недискриминации, связанных с квалифицированными планами. План SIMPLE может быть настроен как план SIMPLE IRA, с использованием IRA или как часть плана 401(k) (план SIMPLE 401(k))

Активы плана увеличиваются без уплаты налогов до тех пор, пока они не будут распределены.

Кто может участвовать в программе SIMPLE?

Участвовать в плане SIMPLE могут только соответствующие сотрудники.

Сотрудник, имеющий право на участие, — это сотрудник, который:

  • получил компенсацию в размере не менее 5000 долларов США в течение любых двух лет, предшествующих текущему календарному году, и
  • Вполне разумно ожидать, что он получит не менее 5000 долларов в течение текущего календарного года.

Для целей пенсионного плана срок Работник включает в себя самозанятое лицо, получившее трудовой доход.

Создание плана SIMPLE

Только работодатели, у которых было 100 или менее сотрудников, получивших компенсацию в размере 5000 долларов США или более от работодателя за предыдущий год, могут создать план SIMPLE.

Наемные работники включают самозанятых лиц, получающих трудовой доход, и наемных работников.

План SIMPLE можно настроить одним из следующих способов:

  • Использование SIMPLE IRA (план SIMPLE IRA)
  • В рамках плана 401(k) (план SIMPLE 401(k))

Планы SIMPLE могут поддерживаться только на основе календарного года.

SIMPE IRAs

Форму 5304-SIMPLE или форму 5305-SIMPLE можно использовать для настройки плана SIMPLE IRA.

Когда использовать форму 5304-SIMPLE:

Используйте форму 5304-SIMPLE, если вы разрешаете каждому участнику плана выбирать финансовое учреждение для получения своих взносов.

Когда использовать форму 5305-SIMPLE:

Используйте форму 5305-SIMPLE, если вы требуете, чтобы все взносы по плану SIMPLE-IRA изначально депонировались в назначенном финансовом учреждении (например, в банках, страховых компаниях).

Имеющие право сотрудники

Согласно плану SIMPLE IRA, SIMPLE IRA должен быть создан для каждого правомочного сотрудника.

Подходящим сотрудником является тот, кто:

  • Получил компенсацию в размере не менее 5000 долларов США в течение любых 2 лет, предшествующих текущему календарному году, и
  • Вполне разумно ожидать, что он получит не менее 5000 долларов в течение текущего календарного года.

Сотрудники могут отчислять часть своей заработной платы на собственный счет SIMPLE IRA (взносы на сокращение заработной платы).

После того, как вы настроите план SIMPLE IRA, вы должны продолжать соответствовать лимиту в 100 сотрудников каждые лет, в течение которых вы поддерживаете план, если только вы не имеете права на льготный период.

Льготный период:

Льготный период предоставляется, если вы поддерживаете план SIMPLE IRA не менее одного года и не достигаете предела в 100 сотрудников в следующем году.

В рамках льготного периода будет считаться, что вы соответствуете лимиту в 100 сотрудников на два календарных года сразу после календарного года, для которого вы в последний раз его достигли.

Когда устанавливать план SIMPLE

Вы можете настроить план SIMPLE в любое время с 1 января по 1 октября календарного года.

Новые работодатели:

Если вы являетесь новым работодателем, чей бизнес начался после 1 октября, вы можете создать план ПРОСТОЙ, как только это станет возможным с административной точки зрения.

Объяснение урока: Преобразования комплексной плоскости

В этом объяснении мы узнаем, как переводить и вращать комплексное число в комплексной плоскости.

Когда мы рассматриваем преобразование комплексной плоскости, мы имеем в виду функции, которые отображают двумерное пространство в двумерное пространство. При первом впечатлении может быть трудно понять, как думать о таких функциях и как их интерпретировать. Трудность возникает из-за того, что наиболее распространенные методы, которые мы используем для понимания реальных функций, имеют тенденцию падать. когда мы пытаемся понять функции, отображающие два измерения в два измерения. Этот объяснитель представит ряд методов, которые мы используем понимать сложные функции.

Мы начнем с нескольких простых примеров, чтобы представить методы, которые мы используем.

Пример 1. Трансляции комплексной плоскости

Найдите уравнение образа |𝑧|=2 при преобразовании комплексной плоскости 𝑇∶𝑧↦𝑧+1+𝑖.

Ответ

Мы рассматриваем преобразование 𝑇 из 𝑧-плоскости в другую комплексную плоскость, которую будем называть 𝑤-плоскость. Тогда мы можем представить преобразование как 𝑤=𝑧+1+𝑖.

Мы можем найти уравнение для образа |𝑧|=2, сначала выразив 𝑧 через 𝑤 следующим образом: 𝑧=𝑤−1−𝑖.

Теперь мы можем подставить это в уравнение |𝑧|=2, которое дает |𝑤−1−𝑖|=2.

Представляет собой окружность радиусом 2 с центром в точке, представленной комплексным числом 1+𝑖. Мы можем представить как 𝑧-плоскость и 𝑤-плоскость следующим образом.

Предыдущий пример знакомит нас с одним из ключевых методов, которые мы используем для понимания преобразований сложной плоскости: рассматривая изображение различных кривых при преобразовании. Понимание эффекта данного преобразования на кругах и линиях поможет часто дают нам разумное представление о том, что делает преобразование. В более общем смысле, Рассмотрение эффекта преобразования кривых и областей — это метод, который мы используем для визуализации более сложных типов преобразования.

Кроме того, в предыдущем примере показано, что преобразование в форме 𝑇∶𝑧↦𝑧+𝑧, где 𝑧=𝑥+𝑦𝑖 — константа (иногда описывается как преобразование 𝑤=𝑧+𝑧), представляет перевод вектором 𝑥𝑦.

В следующем примере мы будем рассматривать преобразования в виде 𝑤=𝑘𝑧, где 𝑘∈ℝ.

Пример 2: растяжения комплексной плоскости

Найдите уравнение образа |𝑧|=1 при преобразовании комплексной плоскости 𝑇∶𝑧↦12𝑧.

Ответ

Мы рассматриваем преобразование 𝑇 из 𝑧-плоскости в другую комплексную плоскость, которую будем называть 𝑤-плоскость. Мы можем представить это преобразование как 𝑤=12𝑧.

Мы можем найти уравнение для образа |𝑧|=1, сначала выразив 𝑧 через 𝑤 следующим образом: 𝑧=2𝑤.

Теперь мы можем подставить это в уравнение |𝑧|=1, которое дает |2𝑤|=1.

Используя свойства модуля, мы можем переписать это как |2||𝑤|=1, что эквивалентно |𝑤|=12.

Представляет собой окружность радиусом 12 с центром в начале координат. Мы можем представить как 𝑧-плоскость и 𝑤-плоскость следующим образом.

В предыдущем примере показано, что преобразования вида 𝑇∶𝑧↦𝑘𝑧, где 𝑘∈ℝ — константа, являются расширениями на масштабный коэффициент 𝑘. Хотя это верное утверждение, строго говоря, предыдущий пример недостаточно для демонстрации этого. Мы видели, что эти преобразования отображают окружности с центром в начала координат на другие окружности с центром в начале координат с масштабированным радиусом. Однако можно было бы что преобразование также повернуло точки на плоскости. Хотя в данном случае это не так, продемонстрируйте, что, как правило, мы должны рассматривать изображения как точек, так и окружностей, чтобы иметь лучшее представление о том, что делает преобразование.

Пример 3: Вращения комплексной плоскости

Найдите уравнение для образа arg(𝑧)=𝜃 при преобразовании 𝑇∶𝑧↦𝑒𝑧 который отображает 𝑧-плоскость в 𝑤-плоскость.

Ответ

Мы можем найти уравнение для образа arg(𝑧)=𝜃, сначала выразив 𝑧 через 𝑤 следующим образом: 𝑧=𝑤𝑒.

Теперь мы можем подставить это в уравнение arg(𝑧)=𝜃, которое дает arg𝑤𝑒=𝜃. 

Используя свойства аргумента, мы можем переписать это как аргарг(𝑤)+𝑒=𝜃.

Поскольку arg𝑒=−𝜑, мы можем упростить это до аргумент(𝑤)=𝜃+𝜑.

Это полупрямая, конечная точка которой находится в начале координат, образующая угол 𝜃+𝜑 с положительной действительной осью.

Предыдущий пример показал нам, что при преобразовании 𝑤=𝑒𝑧, полупрямая изображения в начале координат, образующая угол 𝜃 к действительной оси представляет собой полуось в начале координат, которая образует угол 𝜃+𝜑. Это показывает, что преобразование повернуло плоскость на 𝜑. Более того, мы знаем, что он не масштабировал линию, поскольку модуль 𝑒 равен единице.

Обратите внимание, что если бы мы рассмотрели изображение круга в предыдущем примере, мы бы обнаружили, что его изображением будет круг в 𝑤-плоскости с тем же центром и радиусом. Это было бы не очень познавательно. Вот почему нам часто приходится рассматривать изображение как линий, так и окружностей. чтобы получить более четкое представление о том, что делает данное преобразование.

Объединяя результаты примеров 2 и 3, мы видим, что умножение на общий комплексное число 𝑧=𝑟𝑒 можно понимать как комбинацию преобразования, которое мы получить путем умножения на действительное число 𝑟, которое представляет собой расширение на масштабный коэффициент 𝑟, а преобразование, полученное умножением на 𝑒, что представляет собой поворот против часовой стрелки вокруг начала координат на угол 𝜃.

Основное преобразование комплексной плоскости

Пусть 𝑧=𝑥+𝑦𝑖, где 𝑥,𝑦∈ℝ постоянные.

  1. Преобразование 𝑇∶𝑧↦𝑧+𝑧 представляет собой перевод вектором 𝑥𝑦.
  2. Преобразование 𝑇∶𝑧↦𝑧𝑧 представляет собой расширение на масштабный коэффициент |𝑧| и вращение против часовой стрелки вокруг начала координат с помощью arg(𝑧).

Комбинируя эти преобразования, можно создавать более сложные преобразования. Например, мы можем понимать преобразование формы 𝑇∶𝑧↦𝑧𝑧+𝑧 как композицию преобразований 𝑇∶𝑧↦𝑧𝑧 и 𝑇∶𝑧↦𝑧+𝑧. То есть мы можем понять это будет расширение на масштабный коэффициент |𝑧| с вращением против часовой стрелки вокруг начала координат на arg(𝑧), с последующим перевод вектором, представляющим комплексное число 𝑧.

В следующих нескольких примерах мы рассмотрим составное преобразование этой формы.

Пример 4. Составные преобразования комплексной плоскости

Найдите уравнение для изображения полупрямой arg(𝑧−4+5𝑖)=𝜋2 при преобразовании 𝑇∶𝑧↦𝑖𝑧−3−𝑖.

Ответ

Мы рассматриваем преобразование 𝑇 из 𝑧-плоскости в другую комплексную плоскость, которую будем называть 𝑤-плоскость. Мы можем представить это преобразование как 𝑤=𝑖𝑧−3−𝑖.

Мы можем найти уравнение для образа arg(𝑧−4+5𝑖)=𝜋2, сначала выразив 𝑧 через 𝑤 следующим образом: 𝑧=𝑤+3+𝑖𝑖.

Подставляя это в уравнение arg(𝑧−4+5𝑖)=𝜋2, получаем arg𝑤+3+𝑖𝑖−4+5𝑖=𝜋2.

Выражая предмет спора одной дробью, имеем аргумент𝑤+3+𝑖−4𝑖+5𝑖𝑖=𝜋2 который мы можем упростить до arg𝑤−2−3𝑖𝑖=𝜋2.

Используя свойства аргумента, мы можем переписать это как аргумент(𝑤−2−3𝑖)−(𝑖)=𝜋2.

Так как arg(𝑖)=𝜋2, мы имеем аргумент(𝑤−2−3𝑖)=𝜋.

Это полупрямая, конечная точка которой находится в точке 3+3𝑖, образующей угол 𝜋 с положительной горизонталью. Мы можем интерпретировать это преобразование как комбинацию двух преобразований 𝑇, вращение против часовой стрелки вокруг начало координат на 𝜋2 радиана, а 𝑇 — перенос на вектор −3−1. Наглядно это можно представить следующим образом.

Пример 5: Составные преобразования комплексной плоскости

Найдите уравнение образа |𝑧−2|=3 при преобразовании 𝑧-плоскости на 𝑤-плоскость, заданную 𝑤=𝑖(2𝑧+2).

Ответ

Начнем с выражения 𝑧 через 𝑤 следующим образом: 𝑧=−𝑖𝑤−22.

Теперь мы можем подставить это в уравнение |𝑧−2|=3, чтобы найти уравнение (в терминах 𝑤) для образа этого места при заданном преобразовании. Следовательно, |||−𝑖𝑤−22−2|||=3.

Выражая предмет модуля в виде одной дроби, имеем |||−𝑖𝑤−62|||=3.

Вынося −𝑖 из числителя, мы имеем |||−𝑖2(𝑤−6𝑖)|||=3.

Теперь мы можем использовать свойства модуля, чтобы переписать это как |||−𝑖2||||𝑤−6𝑖|=3.

Так как |||−𝑖2|||=12, мы можем выразить это как |𝑤−6𝑖|=6.

Это круг радиусом 6 с центром в точке 6𝑖. Мы можем интерпретировать это преобразование как комбинацию трех преобразований: 𝑇, расширение с центром в начале координат с масштабным коэффициентом 2, за которым следует 𝑇, перенос вектором 20, за которым следует 𝑇, поворот против часовой стрелки вокруг начала координат на 𝜋2 радиана. Наглядно это можно представить следующим образом.

В последнем примере рассмотрим преобразование, которое, в отличие от рассмотренных нами преобразований до сих пор не отображает прямые линии в прямые линии, и, следовательно, более сложно получить понимание эффекта трансформации. Однако, используя изученные нами приемы, мы можем рассмотрите его влияние на линии и круги и, в результате, начните создавать картину того, что делает преобразование.

Пример 6: Преобразования комплексной плоскости

Преобразование, переводящее плоскость 𝑧 в плоскость 𝑤, задается выражением 𝑤=𝑧.

  1. Найдите декартово уравнение для образа |𝑧|=8 при преобразовании.
  2. Найдите декартово уравнение для образа Re(𝑧)=4.
  3. Найдите декартово уравнение для образа Im(𝑧)=4.

Ответ

Для точек 𝑧-плоскости обозначим действительную и мнимую части как 𝑥 и 𝑦 соответственно, тогда как для плоскости 𝑤 мы будем обозначать их 𝑢 и 𝑣.

Часть 1

Сначала найдем комплексное уравнение для образа |𝑧|=8 в 𝑤-плоскость; затем мы преобразуем его в декартово уравнение относительно 𝑢 и 𝑣. Мы определяем 𝑤=𝑧. Взяв модуль обеих частей этого уравнения, мы имеем |𝑤|=|𝑧|.

Используя свойства модуля, мы можем переписать это как |𝑤|=|𝑧|=|𝑧||𝑧|.

Учитывая тот факт, что мы хотели бы найти образ |𝑧|=8, мы можем просто заменить |𝑧| с 2 в приведенном выше уравнении, что дает |𝑤|=64.

Следовательно, образ |𝑧|=8 при преобразовании равен |𝑤|=64. Поскольку это круг радиусом 64 с центром в начале координат, мы можем дать декартово уравнение этого как 𝑢+𝑣=64.

Мы можем визуализировать это следующим образом.

Часть 2

Точки в 𝑧-плоскости, удовлетворяющие Re(𝑧)=4 все можно записать в виде 𝑧=4+𝑦𝑖. Чтобы рассмотреть образ этого при преобразовании 𝑤=𝑧, подставим это в уравнение следующим образом: 𝑤=(4+𝑦𝑖).

Раскрывая скобки, имеем 𝑤=(16−𝑦)+8𝑦𝑖.

Поскольку 𝑤=𝑢+𝑣𝑖, мы можем приравнять действительную и мнимую части, чтобы получить два одновременных уравнения 𝑢=16−𝑦,𝑣=8𝑦.

Чтобы получить декартово уравнение из этих двух уравнений, мы хотели бы исключить 𝑦. Из второго уравнения имеем 𝑦=𝑣8. Мы можем подставить это в первое уравнение, чтобы получить 𝑢=16−𝑣8=16−𝑣64.

Мы можем визуализировать это следующим образом.

Часть 3

Все точки 𝑧-плоскости, удовлетворяющие Im(𝑧)=4 можно записать в виде 𝑧=𝑥+4𝑖. Подставляя это в уравнение 𝑤=𝑧, мы имеем 𝑤=(𝑥+4𝑖).

Раскрывая скобки, имеем 𝑤=𝑥−16+8𝑥𝑖.

Поскольку 𝑤=𝑢+𝑣𝑖, мы можем приравнять действительную и мнимую части, чтобы получить два одновременных уравнения 𝑢=𝑥−16,𝑣=8𝑥.

Чтобы получить декартово уравнение из этих двух уравнений, мы хотели бы исключить 𝑥. Из второго уравнения имеем 𝑥=𝑣8. Мы можем подставить это в первое уравнение, чтобы получить 𝑢=𝑣8−16=𝑣64−16.

Мы можем представить это следующим образом.

Как мы видели в предыдущем примере, понимание эффекта трансформации линий и кругов помогает нам понять его общий эффект на сложном плане, даже в случае более общих преобразований. Есть много других техник, полезных для достижения этого понимания, например, рассмотрение прообраза линий и окружностей, цветные карты, векторные поля и обнаружение фиксированных точек преобразования.

Ключевые точки

  • Мы можем получить представление о преобразованиях на комплексной плоскости, рассматривая их влияние на линии и окружности.
  • Для комплексного числа 𝑧=𝑥+𝑦𝑖, где 𝑥,𝑦∈ℝ, преобразование 𝑇∶𝑧↦𝑧+𝑧 представляет перенос вектором 𝑥𝑦.
  • Преобразование 𝑇∶𝑧↦𝑧𝑧 представляет собой расширение на масштабный коэффициент |𝑧| и вращение против часовой стрелки вокруг начала координат с помощью arg(𝑧).
  • Составное преобразование может быть создано путем составления нескольких преобразований. Мы можем понять их влияние, рассмотрев эффект каждого преобразования по очереди.
  • Чтобы получить представление о более сложных преобразованиях, таких как 𝑇(𝑧)=𝑧, мы также можем рассмотреть как он отображает линии и круги. Однако понять точную природу трансформации, как правило, будет сложнее.

Как строить графики комплексных чисел

Все дополнительные ресурсы по геометрии

6 Диагностические тесты 57 практических тестов Вопрос дня Карточки Учитесь по концепции

← Предыдущая 1 2 Следующая →

Расширенная справка по геометрии » Координатная геометрия » График » Как изобразить на графике комплексные числа

Точка А представляет собой комплексное число. Его положение задается каким из следующих выражений?

Возможные ответы:

Правильный ответ:

Объяснение:

Комплексные числа могут быть представлены на координатной плоскости путем сопоставления действительной части с осью x и мнимой частью с осью y. Например, выражение может быть представлено графически точкой.

Здесь нам дают график и просят написать соответствующее выражение.

 не только правильно идентифицирует x-координату с действительной частью, а y-координату с мнимой частью комплексного числа, но и включает необходимое .

 правильно идентифицирует координату x с действительной частью и координату y с мнимой частью комплексного числа, но не включает необходимое .

 неверно идентифицирует координату y с действительной частью, а координату x с мнимой частью комплексного числа.

 неверно идентифицирует координату y с действительной частью, а координату x с мнимой частью комплексного числа. Он также не включает необходимые .

Сообщить об ошибке

Какой из следующих графиков представляет выражение ?

Возможные ответы:

Комплексные числа не могут быть представлены на координатной плоскости.

Правильный ответ:

Объяснение:

Комплексные числа могут быть представлены на координатной плоскости путем сопоставления действительной части с осью x и мнимой частью с осью y. Например, выражение может быть представлено графически точкой.

Здесь нам дается комплексное число  и предлагается изобразить его на графике. Мы представим действительную часть на оси x и мнимую часть на оси y. Обратите внимание, что коэффициент  равный ; это то, что мы будем отображать на оси Y. Правильные координаты .

 

Сообщить об ошибке

Укажите точку пересечения параболы с помощью уравнения . Округлите до десятых, если применимо.

Возможные ответы:

Парабола не имеет -пересечения.

Правильный ответ:

Парабола не имеет -пересечения.

Объяснение:

 -координата(ы) -перехвата(ов) являются реальным решением(ями) уравнения . Мы можем использовать квадратную формулу, чтобы найти любые решения, задавая — коэффициенты выражения.

Проверка дискриминанта, однако, доказывает, что в этом нет необходимости.

Поскольку дискриминант отрицателен, действительных решений нет, поэтому парабола не имеет -пересечений.

Сообщить об ошибке

В каком квадранте находится комплексное число   ?

Возможные ответы:

Правильный ответ:

Объяснение:

При построении комплексного числа мы используем набор действительно-мнимых осей, в которых ось X представлена ​​действительной составляющей комплексного числа, а ось Y представлена ​​мнимой составляющей комплексного числа. количество. Действительный компонент равен   , а мнимый компонент равен  , так что это эквивалентно построению точки    на наборе декартовых осей. Нанося комплексное число на набор действительно-мнимых осей, мы перемещаем    влево в направлении x и    вверх в направлении y, что помещает нас во второй квадрант, или с точки зрения римских цифр:

Сообщить об ошибке

В каком квадранте находится комплексное число   ?

Возможные ответы:

Правильный ответ:

Объяснение:

Если бы мы изобразили данное комплексное число на наборе действительно-мнимых осей, мы бы изобразили действительное значение комплексного числа как координату x, а мнимое значение комплексного числа — как координату y. Потому что данное комплексное число выглядит следующим образом:

По сути, мы делаем то же самое, что и построение точки    на наборе декартовых осей. Мы перемещаем    единиц вправо в направлении x и    единиц вниз в направлении y, что помещает нас в четвертый квадрант, или с точки зрения римских цифр:

Сообщить об ошибке

В каком квадранте находится комплексное число   ?

Возможные ответы:

Правильный ответ:

Объяснение:

Если бы мы изобразили данное комплексное число на наборе действительно-мнимых осей, мы бы изобразили действительное значение комплексного числа как координату x, а мнимое значение комплексного числа — как координату y. Потому что данное комплексное число выглядит следующим образом:

По сути, мы делаем то же самое, что и построение точки    на наборе декартовых осей. Мы перемещаемся на    единиц влево от начала координат в направлении x и на    единиц вниз от начала координат в направлении y, что помещает нас в третий квадрант, или с точки зрения римских цифр:

Сообщить об ошибке

В каком квадранте находится комплексное число   ?

Возможные ответы:

Правильный ответ:

Объяснение:

Если бы мы изобразили данное комплексное число на наборе действительно-мнимых осей, мы бы изобразили действительное значение комплексного числа как координату x, а мнимое значение комплексного числа — как координату y. Потому что данное комплексное число выглядит следующим образом:

По сути, мы делаем то же самое, что и построение точки    на наборе декартовых осей. Мы перемещаемся на    единиц вправо от начала координат в направлении x и на    единиц вверх от начала координат в направлении y, что помещает нас в первый квадрант, или с точки зрения римских цифр:

Сообщить об ошибке

В комплексе плоскости, какое число представляет эта точка?

Возможные ответы:

Правильный ответ:

Объяснение:

В комплексной плоскости ось x представляет действительную часть комплексного числа, а ось y представляет мнимую часть. Показанная точка — (8,3), поэтому действительная часть равна 8, а мнимая часть — 3, или 8+3i.

Сообщить об ошибке

Какое комплексное число представлено на графике ниже?

Возможные ответы:

Правильный ответ:

Объяснение:

Для ответа мы должны знать, что ось x — это реальная ось, а ось y — воображаемая ось. Мы можем видеть, что мы прошли 2 пробела по оси x или в реальном направлении и -3 пробела по оси y или воображаемом направлении, чтобы дать нам ответ 2-3i.

Сообщить об ошибке

Найти,

 

Возможные ответы:

Правильный ответ:

4 Объяснение:

Определение абсолютного значения на координатной плоскости — это расстояние от начала координат до точки.